What is MTF
Modulation Transfer Function (MTF) of a lens is an important indicator of its performance. Both lens designers and users need to have a deep understanding of MTF.
1. What is MTF?
The function of the lens is to image the object on the sensor. An object is composed of countless points. The image formed by every single point of the object will be positioned on the corresponding image point. Meanwhile, it will be weighted according to the brightness of the original target at these positions, leading to a continuous image function called "g". Unfortunately, this long formula is quite obscure.
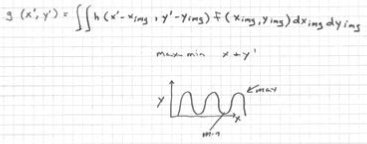
What does the formula really stand for? In other words, what kind of phenomenon does it describe? Following is illustration by several intuitive examples.
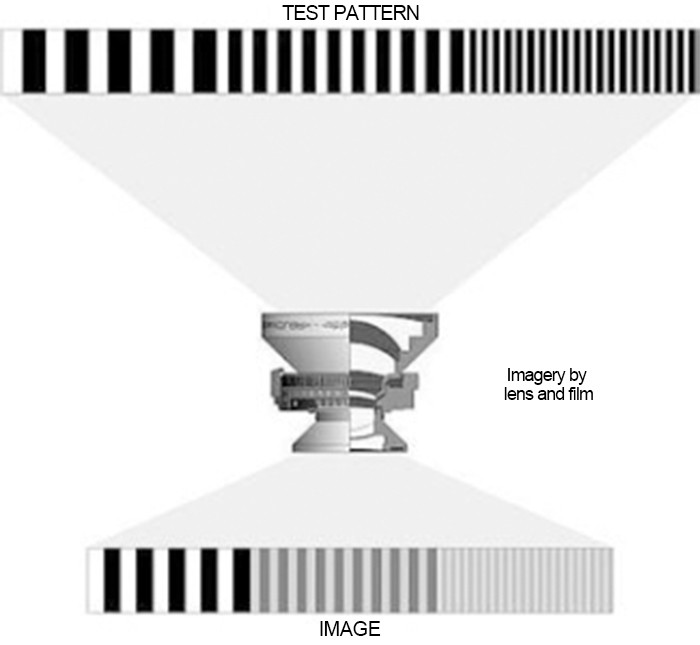
The stripes of the pattern above (representing objects) are black and white (high contrast). From left to right, the spatial frequency of the stripes gradually increases (the stripes become denser).
The object passes through the lens and is imaged on the sensor. We can find that the large stripes in low resolution are still black and white after imaging. They are easily transferred by the lens to the sensor. As the frequency increases, the stripes become denser and the image becomes grayer, and the contrast between them becomes increasingly smaller. It no longer has perfect black and white, and even black and white are indistinguishable.
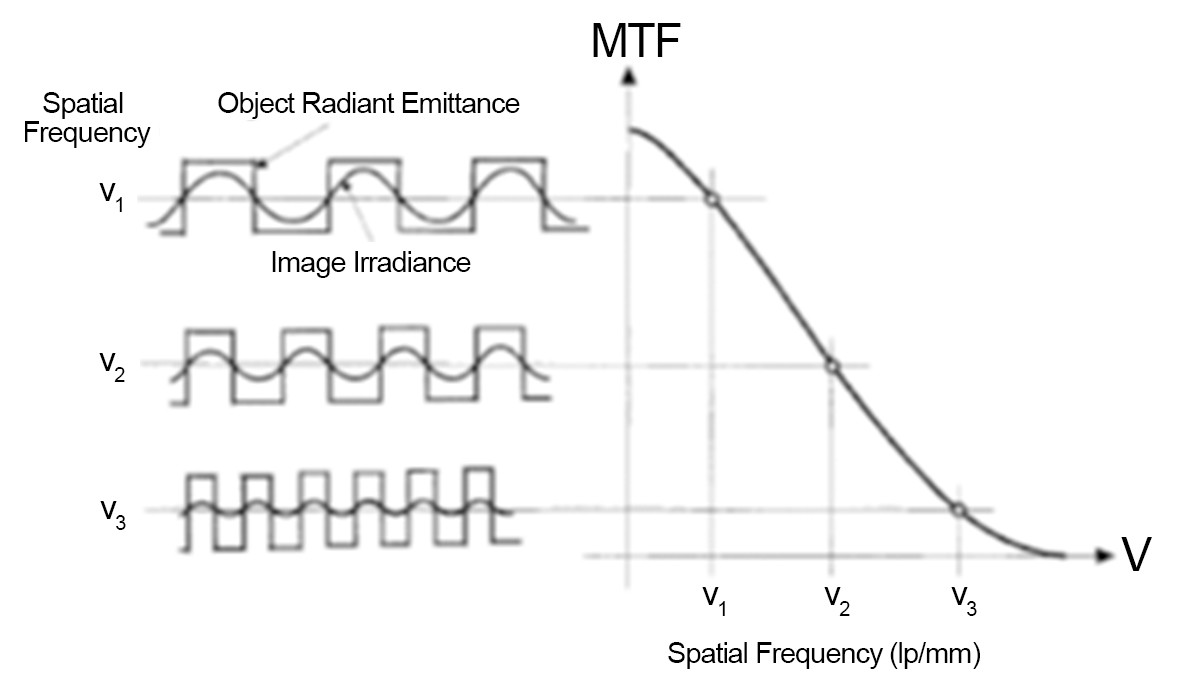
This phenomenon can be described mathematically on the "luminance distribution". The black is 1 and white is 0. At medium contrast, the brightness decreases with the grayscale of the image. The brightness distribution gets smaller and smaller until you cannot distinguish the difference between bright and dark. The right is a typical MTF curve. All MTF curves are of similar shape like this. They all have a cut-off frequency (although the cut-off frequency may be different for each lens. The cutoff frequency is related to the aperture of the lens). Then, MTF will tell you how well the lens replicates the image.
2. How to interpret MTF?
Lens imaging is affected by the orientation of an object in space. For example, the pattern stripes mentioned can be horizontal or vertical. That is the Tangential and Sagittal in optical terminology. The MTF curve describes the imaging capability of the lens in both the Tangential (T) and Sagittal (S). It helps optical engineers avoid designing lenses that perform well in one direction but poorly in another.
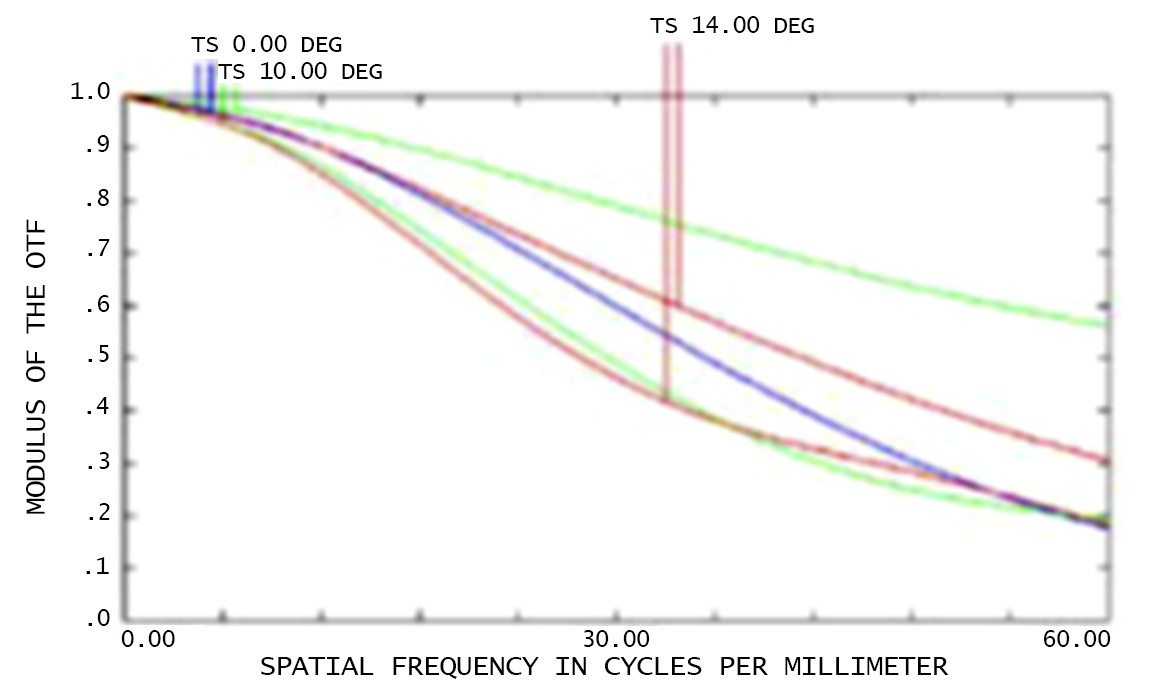
The figure above is a classic MTF graph. The abscissa is spatial frequency in cycles per millimeter and the ordinate is modulus of the OTF. MTF is a function of frequency, so as the frequency increases, the MTF value becomes smaller.
In the top left of the figure, "TS0.00 DEG", T stands for Tangential and S stands for Sagittal. The MTF curve with a FOV of 0° is a blue line, which is what we call "on the axis". There is no difference between Tangential or Sagittal.
Next, "TS 10.00 DEG" is the MTF curve representing a FOV of 10° (green curve). The MTF in this FOV differs greatly in the T and S directions (@60lp, T0.2, S0.68). It means that the lens has relatively severe astigmatism. That is, in one focal point, imaging performs obviously better in one direction than in the other. When the ratio of them is greater than 2:1, we need to consider the effect of astigmatism on the system. Look at the MTF of the 14° field of view, the difference between the two directions of T and S is not so obvious.
Although the maximum FOV shown in the graph is only 14°, in fact, the maximum field of view of this lens is 28°. Generally, the lens is recognized to be rotationally symmetric.
To sum up, the classic MTF curve shows us how well a lens performs at a specific frequency (the number of line pairs contained per millimeter). The higher the MTF value, the better the lens can replicate the object; the lower the MTF value, the worse the lens's ability to replicate the object.
3. How to judge the availability of a lens?
It is essential for optical engineers or lens users to judge whether the lens matches the sensor.
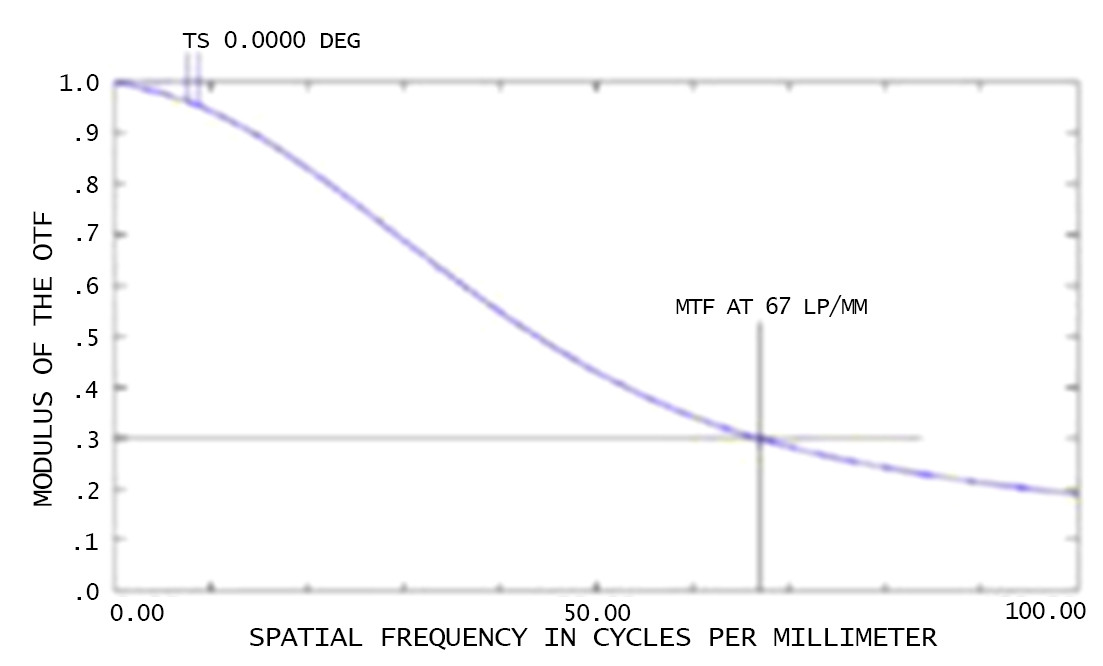
Typically, we choose lenses with an MTF greater than 0.3 at Nyquist frequencies. It is a reliable experience that lenses will not become a limitation of the whole system. Thus, do not be distracted by MTF above the Nyquist frequency, which is not the point of lens design or use. If you are wondering, is the MTF at Nyquist 0.3 or higher? When you ask this question, you already have a lens to choose from that will not affect system performance - of course, the higher the MTF, the better performance.
4. Kindly reminder
At different apertures and working distances, the same lens has different optical performance (MTF). Thus, the first thing to figure out is the conditions of use regarding imaging needs before evaluating a lens.
